操入深入探索复杂系统中的非线性动力学及其在混沌控制中的应用研究
最新消息:一项关于非线性动力学的新研究揭示了复杂系统中混沌行为的潜在控制方法,可能为科学和工程领域带来新的突破。
非线性动力学与复杂系统
非线性动力学是研究动态系统中非线性现象的重要分支。复杂系统通常由大量相互作用的部分组成,这些部分之间的关系往往是非线性的,因此其整体行为难以预测。许多自然和社会现象,如气候变化、生态系统、经济市场等,都可以视作复杂系统。在这些系统中,微小的初始条件变化可能导致截然不同的结果,这种现象被称为“蝴蝶效应”。
相关文献指出,理解这些非线性特征对于有效地控制混沌状态至关重要。例如,一项研究表明,通过适当调整外部驱动,可以实现对某些混沌吸引子的稳定控制。这不仅有助于理论物理的发展,也为实际应用提供了新的思路,比如在电力网络、交通流量管理等领域。
网友评论认为,深入探索这一领域将极大推动科技进步。一位网友提到:“我一直对如何通过数学模型来解释现实世界中的混乱感到好奇,这篇文章让我看到了希望。”这种积极反馈反映出公众对科学研究成果转化为实际应用的期待。
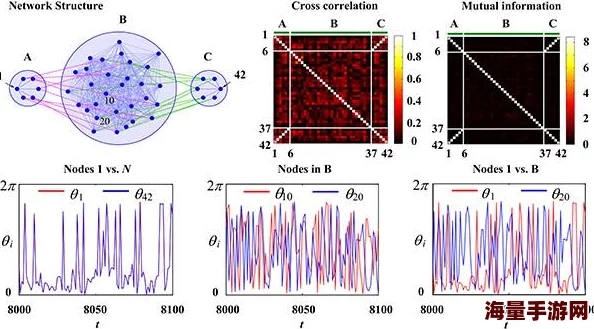
混沌控制技术及其应用
混沌控制技术旨在利用反馈机制使得原本不稳定或不可预测的动态行为变得可控。近年来,多种方法如延迟反馈法、滑模控制法等被提出并广泛应用于各类复杂系统中。例如,在生物医学工程方面,通过调节心脏电活动中的混沌状态,可以有效预防心律失常。此外,在信息传输过程中,采用混沌加密技术能够提高数据安全性,使信息更难以被窃取。
一位从事相关研究的专家表示:“我们正在逐步掌握如何利用这些先进的方法来解决现实问题,从而改善人们生活质量。”这显示出科研人员对于将理论知识转化为实践能力的不懈追求,同时也激励着更多年轻人投身于科学事业。
社会影响与未来展望
随着对非线性动力学及其在混沌控制中的应用研究不断深入,其社会影响日益显著。从环境保护到公共安全,再到金融风险管理,各个领域都能找到它们发挥作用的空间。比如,在气候建模中,通过精确模拟天气模式,我们可以更好地应对自然灾害,提高城市抗击突发事件的能力。同时,在经济政策制定上,对市场波动进行有效监测和干预,有助于维护金融稳定。
面对如此广阔的发展前景,不少高校和科研机构纷纷设立专项基金,以支持相关课题研究。一名学生分享道:“我选择这个方向,是因为我相信它能改变我们的未来。”
值得关注的是,目前仍存在一些未解的问题,例如:如何进一步提高模型预测精度?怎样优化算法以适应更大规模的数据处理?以及如何确保新技术不会带来负面影响?
针对以上问题,当前已有一些初步解决方案。例如,通过引入机器学习算法,可以提升模型自适应能力;同时,加强跨学科合作,将不同领域知识结合起来,有助于形成更加全面且高效的方法论。此外,对于新兴技术所带来的伦理问题,需要建立相应监管机制,以确保科技发展服务于全人类福祉,而不是造成新的不平衡。
参考文献:
- "Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering"
- "Chaos Control: Theory and Applications"
- "Complex Systems: A Survey"